Hey Everyone,
We had a client that purchased some of our anti-crystallization oil. The ratio that our client used still crystallized so we worked together to make sure the formulation was done correctly to ensure the oil didn’t crystallize. We want to share that formulation here. I have written three methods for solving depending on what may be easiest for each individual to understand.
The formula that we ended up using was taken from our other post that detailed different types of formulas that can be used when trying to dose correctly.
---->LOOK here to learn how to dose and formulate correctly
In this example we needed to figure out how much weight of each oil was needed to make sure it did not crystallize. We are solving to create a 1:1 ratio of total CBD molecule to total CBDa.
Method #1
The Data:

Formula: Desired potency / Total Potency x 100%
Total mg CBD = 1,199.40 [ 971.70 + 228 ]
Total Mg CBDa = 737.90
1,199.40 – 737.90 = 461.50 mg of CBDa difference which is our desired potency
Desired Potency: 461.50 mg
Total Potency: 509.90 mg [737.90 – 228]
461.5/509.9 × 100% is .905
This means for every 1g of clients CBD oil, we will add 1.905 of the anti-crystallization oil. Now let’s see how that looks when we plug it back into an example to see if we are right. This example says we will use 100g of CBD oil, and then 1.9057x that for the anti-crystallization oil. We then see that the mg of CBD and CBDa are equal to a 1:1

This can also be written as:
CBD Oil: 34.42%
CBDa Oil: 65.58%
Method #2: Algebra all the way
If you want to dust off your seventh-grade algebra skills, here is another way to figure out the ratios, if the first way is confusing. Luke prefers the above method, but for me I like to see it mathematically in front of me for me to understand, and I find it easier with this way to work with a wide variety of different desired outcomes since it is broken down more fundamentally. Choose your own adventure!
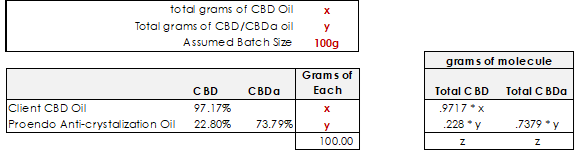
What makes this problem trickier a first is the fact that there is CBD in both oils, but it is still just a simple algebra equation.
We know that there will be x total grams of the client’s CBD oil in the final solution. We know that .9717 * x will give us the ending grams of CBD molecule for that oil
We know that there will be y total grams of non-crystallizing oil in the final solution. We know that there will be .228 * y grams of CBD, and .7379 * y grams of CBDa
We know that the grams of CBD should be equal to the grams of CBDa
When we draw it out in the above format (the right part of the pic), we can easily see that the formula would look like this:
.9717x + .228y = .7379y
Shown in more detail, you could look at it like this:
.9717x + .228y = z
.7379y = z
Therefore, z = z, so .9717x + .228y = .7379y
Step 1: See the two formulas you have
These two formulas are both true, but since there are two variables involved, we can’t initially see what x or y should be.
.9717x + .228y = .7379y
x + y = 100 (we are assuming 100g of total oil will be used)
Step 2: Isolate one variable
x = y = 100
reduces to: y = 100 - x
Step 3: Plug this isolated variable (y) back into the other formula
.9717x + .228(100 - x) = .7379 (100 - x)
.9717x + 22.8 - .228x = 73.79 - .7379x
Then solve for x
1.4816 x = 50.99
x = 34.4155
Step 4: Plug this into your other formula of x+y=100 to find Y
34.4155 + y = 100
y = 65.5845
Method #3 – Goal Seek function in Excel, Instant Answer
If you have Excel, there is a “Goal Seek” function where it will solve algebra problems for you as long as you set it up correctly. The function reads like “This particular cell should be 0, by changing the value in this other cell”.
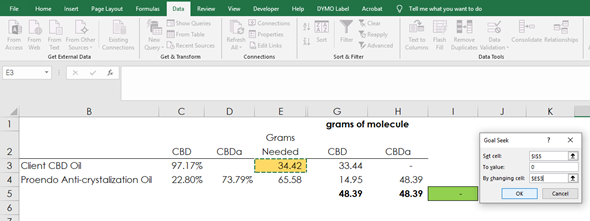
The formula in I5 is calculating the difference between the ending grams of CBD and CBDa (which we want to be zero since we are looking for a 1:1), by adjusting our X variable which is the grams of CBD oil.
If you have any questions or would like to discuss anything specific in more detail, please don’t hesitate to reach out. We would be happy to help.
Cheers,
Gianna